Note: The precious little I know about machine learning I learned from the brilliant Frank Wood, whose talk at the Machine Learning meetup inspired me to finally put together this post. I also worked with my friend Frederik Lang on the material presented here, but the shortcomings remain all my own.
Microsoft’s Kinect sensor is the first large-scale, commercial release of a depth camera device—a camera that can see in 3D. Though depth cameras are not exclusive to Microsoft (and, in fact, the Kinect’s hardware design is licensed from the Israeli company, PrimeSense), Microsoft’s novel use of the device as a game controller is driven by the company’s own software for analyzing its 3D data, including proprietary algorithms for feature selection, scene analysis, motion tracking, skeletal tracking and gesture recognition. Now, suppose we want to do this kind of analysis ourselves. Where do we even begin?
The answer can quickly lead us into deep computer vision and machine learning territory that will send noobs packing. But in this article, we’ll simplify the task, use some pre-existing machinery as a subsystem for our code, and attempt to perform–or at least understand–simple gesture recognition on data from the Kinect. Warning: Some math is involved. If you’re still with me, read on.
What You Need to Proceed
All you need to try out this basic HMM-based gesture recognition technique for yourself is a working install of GNU Octave (which means Matlab should more or less work, as well). I’ve cobbled together some code for applying this technique to 3D point data in Octave, and I’ve included some gesture data (including training and test sets) gathered using a Kinect and OpenNI’s hand-tracking capability as described below.
That said, I do not cover specifically how to get this point data yourself from Kinect/OpenNI (though that is covered in lots of places, so check the forums), and I do not describe how to implement gesture recognition in real time (though I can assure you that it’s do-able by extending the techniques described herein—we’ve done it in Sensecast). My goal is simply to share a working proof-of-concept in the hope that it helps someone. Last time I checked, you can’t find fleshed-out examples of HMM-based gesture recognition on the open Web.
Kinect Gesture Recognition Example Application
To keep the exercise tethered to reality, let’s posit a hypothetical application. The ”operating room” scenario is fairly common “Kinect hacks” fare: Imagine a surgeon who wants to manipulate data and images on a screen without leaving the operating table, touching foreign objects, etc. She wants the screen to respond to a gesture vocabulary that’s intuitive, even personal, and so we’ve decided that the system should be “trainable” and make use of the X-, Y- and Z-axis. Can we make it happen?
Modeling a Gesture
You can readily observe that a gesture such as a hand wave or a fist pump (hey, I’m from New Jersey) can be modeled as a sequence of states:

Statisticians use models to infer truth from observed data. For example, we might want to infer whether or not this douchebag is fist-pumping. A fist-pump model can be developed to give us the probability that he is fist-pumping given the sequence of observation images. Of course, in this case we don’t need a gesture model to tell us that the probability is 100 percent–the douchebag model works just fine.
In any case, to do recognition, we need observations, or data. The “subsystem” we’re going to use here to make observations is not the Kinect depth image but rather the hand-point tracking code implemented in PrimeSense’s open-source OpenNI framework for Kinect and Kinect-like sensors. This approach makes it possible for us to reduce our observation data to sequential 3D points (x, y, z) and focus on the recognition task without processing all those pixels. For us, the data to be analyzed will look more like this:

A fist-pump model can be developed to give us the probability that this douchebag is fist-pumping given the sequence of observation images. Of course, in this case we don’t need a gesture model to tell us that the probability is 100 percent — the douchebag model works just fine.
The typical model for a stochastic (i.e. random) sequence of a finite number of states is called a Markov chain or Markov model, and a physical gesture can be understood as a Markov chain where the true states of the model S = {s1, s2, s3, …, sN } are hidden in the sense that they cannot be directly observed. This type of Markov model is called a Hidden Markov Model (HMM). At each state an output symbol O = {o1 , o2 , o3 , …, oM } (say, the position of the hand) is emitted with some probability, and one state transitions to another with some probability. With discrete numbers of states and output symbols, this model is sometimes called a “discrete HMM” and the set of output symbols the “alphabet.” We learn the emission and transition probabilities while “training” the model with known gesture data (so this is a supervised learning process) and store these values in the emission and transition matrices (more on this below). Each trained model can then be used to determine with what probability a given gesture appears in test data, where the presence or absence of the gesture is unknown. That is, trained HMMs can be used to recognize gestures! Believe it or not, this stuff actually works.
HMMs for Gesture Recognition
The task of gesture recognition shares certain similarities with other recognition tasks, such as speech recognition and biometrics: given a signal varying in time, how can we identify variations in the signal that fit some known model? Though alternatives have been attempted (e.g. Dynamic Programming, or DP-matching algorithms), the most successful solutions still tend to involve some kind of feature-based, bottom-up statistical learning, usually Hidden Markov Models. The landmark article on the topic is Rabiner’s “tutorial” on HMMs (PDF), in which he not only describes using HMMs in speech recognition, but also demonstrates the broad application of HMMs to practical tasks of recognition, identification, prediction, etc.. An early effort by Yamato et al. applied discrete HMMs to learning six different tennis strokes, or “actions,” successfully recognizing them in image sequences with more than 90% accuracy . Starner and Pentland demonstrated that explicit gesture recognition focused on American Sign Language could be accomplished in real time using HMMs applied to data from a video camera. Lee and Kim (PDF) developed an HMM-based “threshold model” to address the special challenge in gesture recognition of differentiating gestures from non-gestures in a continuous stream of data. Others have sought to develop more complex models for vision-based gesture recognition by, for example, causally “linking” or “coupling” models for both the left and right hands. A handful of studies have extended gesture recognition to 3D space using sterescopic cameras and wearable sensors.
There are some known shortcomings of the canonical HMM, such as its incapacity to model state durations, something that might be useful to gesture recognition. Still, for this exercise, we’re going to apply a basic, canonical HMM. And we’re going to use what’s called a “left-to-right HMM,” a model constrained in terms of the state transitions that are possible.
From Model to Data and Back
Consider the nature of a hand gesture, such as a circular “O” made as if drawing a circle on a chalkboard without chalk or a board. Isolated in time, the circle gesture has an ideal or canonical form and a noisy, imperfect instantiation in reality, as pictured here:
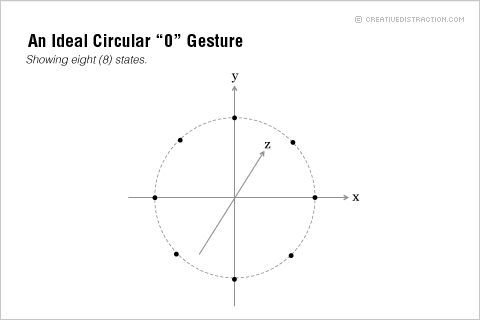
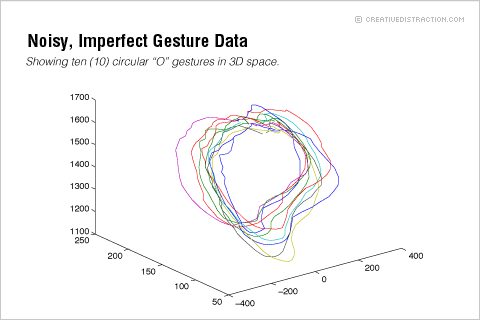
Each colored ring in the “noisy” data above represents an instance of a real circle gesture. (Yes, that’s me twirling my arm in a circle 10 times—I was huffing and puffing at 6 so my apologies for the gradual degeneration in quality.) Now consider that if we’re running a Kinect with the OpenNI hand-tracking code at 30 frames per second, we’ll capture a two-second circle gesture in 60 observations, each observation having three dimensions: x, y, and z. To decide whether a given set of 60 observations contains a circle gesture, we need to first determine the likelihood that the hand passed through the eight states of the canonical gesture in the expected sequence.
Remember that the setup for our discrete HMM is a finite set of M possible output symbols (called the “alphabet”) and a sequence of N hidden states (which the output symbols “reveal” with some probability). To reduce our real gesture data to a workable number of discrete output symbols and states, we can use a clustering algorithm (in this case, I use k-means) to cluster the 3D points of all our training data for circle gesture sequences into, say, N clusters. (That is to say, every point in the training data represents an output symbol that’s closely tied to one of the 8 true states of the model.) We then use the centroids of these clusters to “label” the test data. Because we don’t know whether or not the test data contains the gesture or not, we expand the available alphabet of output symbols to, say, M=12 so that they are not automatically constrained to the 8 that make up the target gesture. (An “X” or “Z” motion with the hand, for example, requires hand positions that aren’t used when making an “O” motion, and these positions should yield different output symbols.)
Looking at the labeled data, we can estimate how likely it is that a hand passed through the 8 clusters in the same sequence as a circle gesture, and if the likelihood is high enough, congratulations, you have yourself a recognized gesture! By normalizing all training and test observations to the origin of the coordinate system, this approach is fairly robust to changes in camera position and orientation. And for reasons beyond the scope of this article (and also over my head!), HMMs are decently scale-invariant, meaning recognition should work regardless of the size of the person performing the gesture.
The Math
Determining whether a sequence of observations fits the model requires us to solve a couple of probability problems. The first can be expressed as the probability of a certain true state i at time step t given the data:
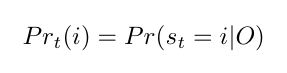
If we can compute this marginal probability at every time step in a sequence, we can predict the hidden states and determine to what degree the data fit our model of a gesture. Recall that our model is a Markov chain, or a sequence of “random” events, so we’re also interested in the transitions between states. We can compute the marginal probabilities of the state being what it is (emission) and changing (transition) at every time step using a message-passing algorithm called the forward-backward algorithm where the messages are computed like:
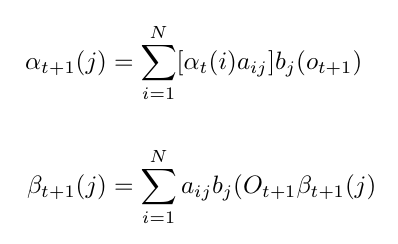
The probability of the model being in a specific state i at time t and the probability of transition from state i to state j at time t can then be estimated:
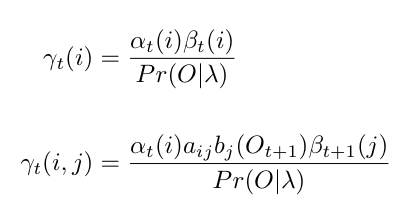
Ultimately, our model is going to encode these probabilities in the transition matrix A and the emission matrix B. After we’ve computed the marginal probabilities at time t as above, we can re-estimate these model parameters using a compelling, easy-to-compute iterative optimization algorithm that was shown by Baum and Welch, the Baum-Welch algorithm, which consists of two update equations, alpha and beta:
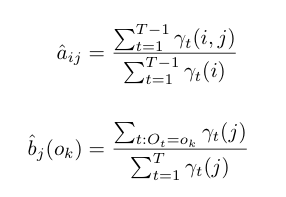
While we need to initialize these model parameters, the most important initialization for a gesture model is the transition matrix because it gives us a chance to constrain the possible transitions. By zeroing out the probabilities at the matrix edges, i.e. the probabilities of jumping between distant states in the model, we can restrict the model to the sequence of adjacent states that constitute a gesture. In other words, we choose a prior that constrains the transition matrix such that state transitions can only occur in one direction and between two adjacent states, also called a left-to-right HMM. Our prior on A therefore looks like this:

The Code
If this math seems incomprehensible, not to worry. You might find it easier to see how it’s all implemented in the Octave/Matlab code. Just run the included sample test.m which gives you the entire process of initializing an HMM, training it on gesture training data where we know a gesture is present (supervised learning), and then testing it on test data. If you run test.m, you should see output similar to this:
<br></br>********************************************************************<br></br>Training 10 sequences of maximum length 60 from an alphabet of size 8<br></br>HMM with 12 hidden states<br></br>********************************************************************
cycle 1 log likelihood = -1248.538144
cycle 2 log likelihood = -982.629625
cycle 3 log likelihood = -732.009407
cycle 4 log likelihood = -696.890070
cycle 5 log likelihood = -689.663383
cycle 6 log likelihood = -685.441817
cycle 7 log likelihood = -674.623979
cycle 8 log likelihood = -598.479502
cycle 9 log likelihood = -530.171032
cycle 10 log likelihood = -522.078143
cycle 11 log likelihood = -521.170559
cycle 12 log likelihood = -520.974759
cycle 13 log likelihood = -520.894473
cycle 14 log likelihood = -520.851012
cycle 15 log likelihood = -520.825580
cycle 16 log likelihood = -520.810292
cycle 17 log likelihood = -520.800933
cycle 18 log likelihood = -520.795098
cycle 19 log likelihood = -520.791392
end
********************************************************************
Testing 10 sequences for a log likelihood greater than -104.157798
********************************************************************
Log likelihood: -48.890827 > -104.157798 (threshold) – FOUND circle GESTURE!
Log likelihood: -49.721725 > -104.157798 (threshold) – FOUND circle GESTURE!
Log likelihood: -49.795951 > -104.157798 (threshold) – FOUND circle GESTURE!
Log likelihood: -51.037861 > -104.157798 (threshold) – FOUND circle GESTURE!
Log likelihood: -53.615149 > -104.157798 (threshold) – FOUND circle GESTURE!
Log likelihood: -49.848664 > -104.157798 (threshold) – FOUND circle GESTURE!
Log likelihood: -46.062106 > -104.157798 (threshold) – FOUND circle GESTURE!
Log likelihood: -47.221862 > -104.157798 (threshold) – FOUND circle GESTURE!
Log likelihood: -47.344446 > -104.157798 (threshold) – FOUND circle GESTURE!
Log likelihood: -44.769018 > -104.157798 (threshold) – FOUND circle GESTURE!
Recognition success rate: 100.000000 percent
The training and test data are just CSVs of x, y, and z data from a bunch of hand gestures, but the data sets are not identical. I actually created them twice, sitting in front of my Kinect, gesturing.
Look at the structure of the data in the data directory, and try tweaking the code in test.m to get a better feel for what’s going on. Note that if you train the HMM on some “Z” gesture data and test it on some “Z” gesture data, it should find the gesture with a decent success rate. But if you train the model on some “Z” gesture data and test it on some circle gesture data, it should find nothing.
Whew! This blog post is inadequate to the task of introducing, explaining and demonstrating HMMs, but I hope it gives you at least enough material to make you a little more dangerous than you were before.